Praca w grupie – najczęściej na taką formę pracy oporni są ci uczniowie, którzy nastawieni są na sukces. Dlaczego? A co będzie jak do jego grupy trafi jakaś trąba matematyczna, która nie pomoże rozwiązać problemu, a jeszcze będzie spowalniać pracę całej grupy?!

Do dzisiaj byłam dumna ze stosowanego sposobu na utrwalanie umiejętności rachunkowych. Uczniowie siadali w małych grupach, na ławce stał metodnik, którym komunikowali się ze mną, czy potrzebują pomocy i liczyli, jak to na matematyce, kupę słupków, działań, równań czy innych algorytmów. Każdy uczeń miał kartę, na której był rysunek, a na nim prawidłowe wyniki. W tle leciała jakaś muzyka, mająca uatrakcyjnić uczniom te mozolne ćwiczenia i ukoić moją skołataną duszę nauczycielską, która nie do końca akceptuję ten szum, hałas w czasie pracy zespołowej.

Tak najczęściej wygląda praca zespołowa na moich lekcjach. Już prawie nie ma marudzenia, że nie chcą być z kimś w grupie jak było to na początku wspólnej pracy. Pamiętam to dobrze, bo był:
- płacz,
- obrażanie się,
- odmowa pracy,
- zakrywanie rękawem swoich zadań,
- każdy sam liczył i nie konfrontował z kolegami rozwiązań,
- nie rozmawiali ze sobą,
- lepszy uczeń wołał mnie, żebym wytłumaczyła słabszemu, sam nie próbował tłumaczyć koledze…
Pamiętam, jak musiałam namawiać tych najlepszych z matematyki uczniów, żeby wytłumaczyli koledze, przekonywałam, że najlepiej się nauczą, kiedy będą komuś tłumaczyli. Dziś zapowiadam „uczenie się na nauczyciela” i każdy wie, że będziemy pracować w grupach. Temu, kto zapomina, o co chodzi, wskazuję na rysnotkę zrobioną przeze mnie na podstawie książki Kotarskiego „Włam się do mózgu”.
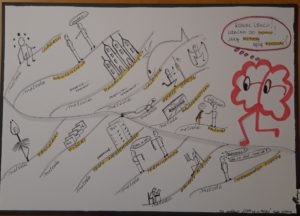
Właśnie rozpoczęłam na stronie www.education.microsoft.com kurs „Nauczanie XXI wieku – praca zespołowa” i mogę podpisać się pod słowami Sokratesa „Wiem, że nic nie wiem”. Dumna ze swoich dotychczasowych zadań edukacyjnych przygotowanych do pracy w grupie dziś, po tym kursie, widzę, że spełniają one tylko pierwsze z czterech najważniejszych aspektów pracy zespołowej :
- uczniowie pracują w grupach
- współdzielą odpowiedzialność za wykonanie zadania,
- podejmują wspólne decyzje,
- jest współzależność między pracami uczniów.
Czyli znów znalazłam coś w swoim warsztacie pracy do poprawki 🙁 Tak, uczyć się trzeba przez całe życie, coś tam muszę pozmieniać w tej pracy zespołowej moich uczniów, żeby również na matematyce rozwijali tę najważniejszą dla nich kompetencję kluczową. Miałam ostatnio okazję opowiadać o swoim warsztacie pracy podczas rady pedagogicznej. Bardzo trudne zadanie, bo wiadomo, „nikt nie jest prorokiem we własnym kraju”, a jeszcze trudniej, kiedy wśród słuchaczy siedzi trzech byłych uczniów, teraz kolegów z pracy. Motywem przewodnim mojego wystąpienia była prezentacja Danuty Sterny, którą miałam okazję wysłuchać dwukrotnie: w Warszawie na I Konferencji OK zeszytu i we Wrocławiu na II spotkaniu grupy FB Ocenianie kształtujące. Dzieliłam się z koleżankami i kolegami swoimi refleksjami na temat:
- jak bardzo mój uczeń jest samosterowny,
- ile z 11 punktów przedstawionych na wykładzie, jeszcze nie potrafię zrealizować na swoich lekcjach i co mi w tym przeszkadza.
Jak mantrę na radzie powtarzałam słowa „Jeżeli, Kasia, Iza, Rafał, moi dawni uczniowie, weszliby na moją lekcję i poczuliby się jakby świat się zatrzymał, bo lekcja matematyki wygląda tak samo, jak za ich czasów, to by znaczyło, że źle uczę”. Metody i sposoby, którymi przekazywałam wiadomości i doskonaliłam umiejętności rachunkowe moich uczniów ponad dwadzieścia lat temu muszą się zmienić, bo dzieci, przed którymi dzisiaj staje, są inne. Niektórzy z nas, nauczycieli, mówią: te dzieci są coraz głupsze. I już się czujemy wytłumaczeni z porażek edukacyjnych naszych uczniów. Potem mówimy: ta podstawa programowa… I już mamy kolejną wymówkę… Dzieci nie są głupsze, neurodydaktycy nic takiego w mózgach współczesnych dzieci nie zauważyli. Dzieci są inne, one nawet tekst w podręczniku czytają inaczej. Jak wskazują badania, ja z pokolenie X, śledzę tekst jakby był wyjustowany, od linijki do linijki, a gałka oczna mojego współczesnego ucznia hula po kartce papieru od góry do dołu i w poprzek. Nasz uczeń zapoznaje się z treścią na kartce jakby oglądał stronę witryny internetowej…
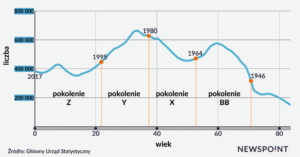
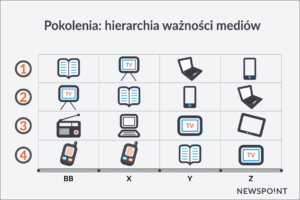
Wystarczy popatrzeć na te dwa slajdy z raportu NEWSPOINT. Trudniej mi, przedstawicielowi pokolenia X, docierać do młodego człowieka z ławki szkolnej. Kiedyś mój uczeń niewiele się ode mnie różnił, oglądał te same programy, seriale w telewizji, słuchał podobnej muzyki… mogłam, stosując różne mnemotechniki odwoływać się do bohaterów telewizyjnych i tłumaczyć. Pamiętam, że rozwiązywanie układów równań metodą podstawiania pomagał mi wytłumaczyć Kloss, potem zastąpił go Bond:)
To jeszcze opowiem coś z mojego matematycznego podwórka, na potwierdzenie, jak bardzo zmieniają się moi uczniowie i jak ja jako nauczyciel muszę zmieniać swoje sposoby nauczania.
Działania na zbiorze liczb całkowitych. Dla niektórych ludzi te działania to jakiś horror. Bo jak są dwie liczy z minusami to czy je dodać, czy odjąć, czy wynik powinien mieć plus, czy wynik zapisać z minusem? W tym roku moi szóstoklasiści poznawali liczby ujemne i bardzo szybko znaleźli je w swoim życiu codziennym – na termometrze – w końcu zimno się zaczęło robić i mróz ściął kałużę, gdy temperatura zeszła poniżej zera. Jeszcze były ujemne punkty w grach, bo stan konta w banku, kiedy się ma debet, już nie były tak oczywisty, że przedstawia się to jako liczby ujemne… Ale kiedy zaczęły się pierwsze działania, stare sposoby tłumaczenia, sprawdzone w innych latach, na innych uczniach, mogłam odłożyć do kosza…
To zobaczcie jak próbowałam wyjaśnić to działanie – 2 – 3=
- jak masz 2 złotych długu u babci i jeszcze pożyczasz od niej 3 złote, to ile masz?
- jeżeli na dworze jest -2 stopni i temperatura spadnie jeszcze o 3 stopnie, to ile jest na termometrze?
- jeżeli masz te same znaki, to oblicz sumę i wynik będzie miał ten sam znak (SSS)
- jeżeli liczby mają ten sam znak, to dodajemy ich wartości bezwzględne i wynik będzie miał ten sam znak
Który ze sposobów wydawał się moim uczniom najbardziej oczywisty? Wiecie jak wyglądały oczy uczniów, kiedy im tak zaczęłam tłumaczyć?

Wtedy, widząc rozpacz i zniechęcenie uczniów, narysowałam działanie i opowiedziałam historyjkę. Protestujący maszerowali, nagle spotkali innych i jak zobaczyli, że mają ten sam sztandar, te same poglądy, postanowili się połączyć i pomaszerować dalej pod wspólnym, takim samym sztandarem. Porównanie do marszów w Dniu Niepodległości i wyborów parlamentarnych samo cisnęło się na usta i pomogło 🙂
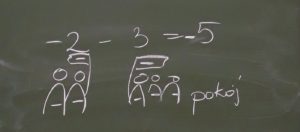
A jak próbowałam wyjaśnić to działanie? – 4 + 5=
- jak masz 4 złotych długu u babci i dostałeś od dziadka 5 złotych, to ile masz?
- jeżeli na dworze jest -4 stopni i temperatura wzrośnie o 5 stopni, to ile jest na termometrze?
- jeżeli masz te różne znaki, to oblicz różnicę i wynik będzie miał znak liczby, która dała pieniądze na reklamę (RRR)
- jeżeli liczby mają różne znaki, to odejmij ich wartości bezwzględne i wynik będzie miał znak tej liczby, której wartość bezwzględna jest większa
Nic nie zadziałało, ale obrazkowa historyjka już tak. Dwie grupy protestujących, każdy ze swoim sztandarem stanęli naprzeciw siebie. Nie byli pokojowo nastawieni, więc ruszyli do walki wręcz, kto zwyciężył, kto został i pod jakim sztandarem?

No powiem, że ten rysunkowy sposób chwycił. Kiedy uczniowie pracowali (w tych jeszcze niedoskonałych) grupach, słyszałam jak sobie tłumaczą:
- nie widzisz, że tutaj jest wojna?
- zobacz leją się, kto został na placu niepokonany?
- tutaj trzeba dodać, bo idą z ta samą flagą, mają takie same poglądy, pokój…
Szóstoklasiści pisali potem pracę pisemną z działań i byłam zachwycona ocenami, wielu dostało pierwszy raz na matematyce 6.

Kiedy pojawiły się inne działania na zbiorze C: dzielenie, mnożenie, potęgowanie, usuwanie nawiasów, moim uczniom nie wystarczyła zasada parzysta liczba minusów, to wynik dodatni, nieparzysta liczba minusów wynik ujemny. Niektórzy domagali się jakieś historyjki i rysunku. I powstała opowieść o wampirze. Każdego przed ugryzieniem wampira ochroni czosnek, a również srebrny krzyżyk. Czy z minusów występujących w dzieleniu, mnożeniu, potęgowaniu, możemy zrobić krzyżyk na wampira? Czy zostanie jakiś minus? Jeśli zostanie minus, to wynik będzie z minusem : )=
Zanim liczyliśmy zadania ze wszystkimi działaniami, narysowaliśmy sobie taką mapę myśli, a na niej wszystkie sposoby, od mnemotechnik, po definicje matematyczne.

Pamiętam rozmowy w gimnazjalnym pokoju nauczycielskim i słowa mojej koleżanki: „Ale ja przecież ciągle się staram, uczę tak samo, z takim samym zapałem, a wychodzi coraz gorzej”. Szukaliśmy wtedy nowych sposobów, bo czuliśmy, że coś nam nauczycielom umyka, nawet najlepsi wśród nas widzieli coraz mniejsze postępy swoich uczniów. Teraz wiem, że słowem kluczem było „uczę tak samo”, a przecież z każdym rokiem mój uczeń był innym człowiekiem, z innymi predyspozycjami i innym postrzeganiem rzeczywistości. Jeżeli uczę, muszę zmieniać sposoby, metody, nie mogę wyciągać swoich zżółkniętych notatek z poprzednich lat i dziwić się, że nie są one atrakcyjne dla kolejnego pokolenia. Oj, dużo pracy przed nami nauczycielami, ciągle musimy się uczyć, doskonalić swój warsztat pracy. Zmierza do nas pokolenie alfa, o których myślą nawet producenci samochodów i umieszczają w siedzeniach aut specjalne kieszonki dla telefonów, żeby nasze pociechy mogły wygodnie oglądać bajki w czasie jazdy. Pokolenie alfa nadchodzi, już jest w przedszkolach! To ja, nauczyciel, idę się uczyć! Szkoleń online jest pełno, polecam te odkryte niedawno na stronie www.education.microsoft.com

